Optimal Control for Pendulum

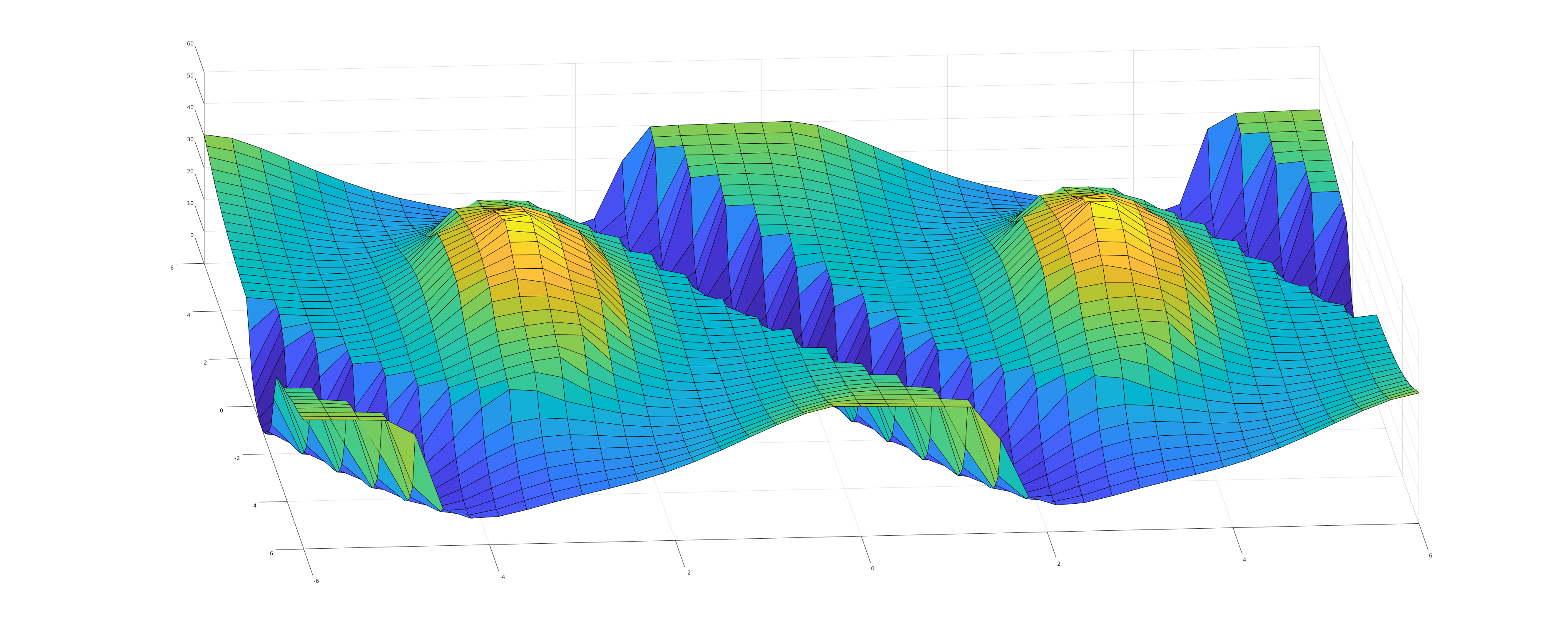
In this project I successfully computed the pendulum's cost-to-go function using a novel contour line approach, achieving an HJB error below 1e-4 both with and without control constraints. We discovered a non-smooth spiral line in the value function, leading to a detailed geometric analysis and a rigorous proof of its existence. Additionally, a 'quasi-discontinuous' line with a unilateral inverse proportional growth rate was identified in the spiral line in control input constrained case. When compared to other optimal cost-to-go functions, our method demonstrated superior outcomes and further guided network performance.

The method we use is backward PMP, equivalent to the Method of Characteristics. The original PMP trajectory is

But PMP is only a neccessary condition, which means we need to choose for the true trajectory. Thanks to the nice property of cost-to-go, we can use the intersection of contour to choose the right one.

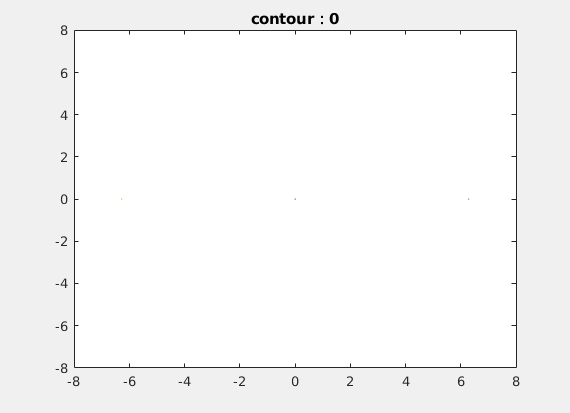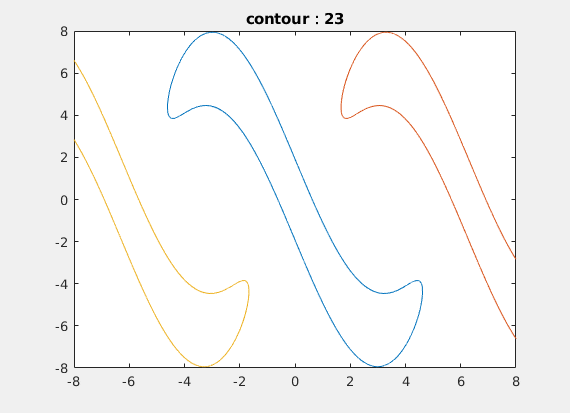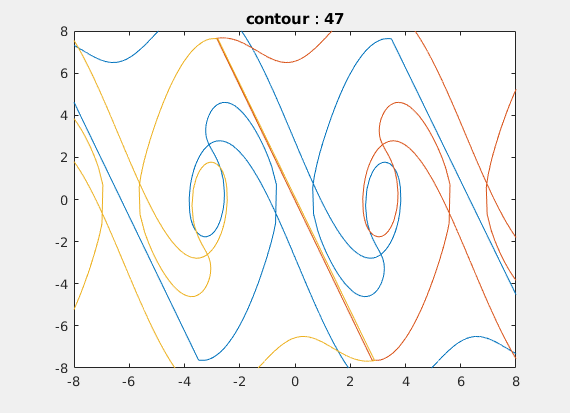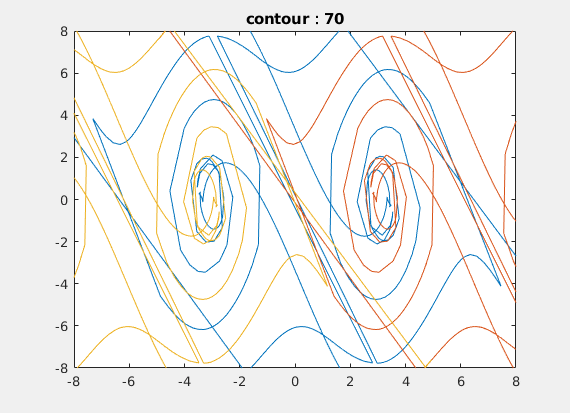
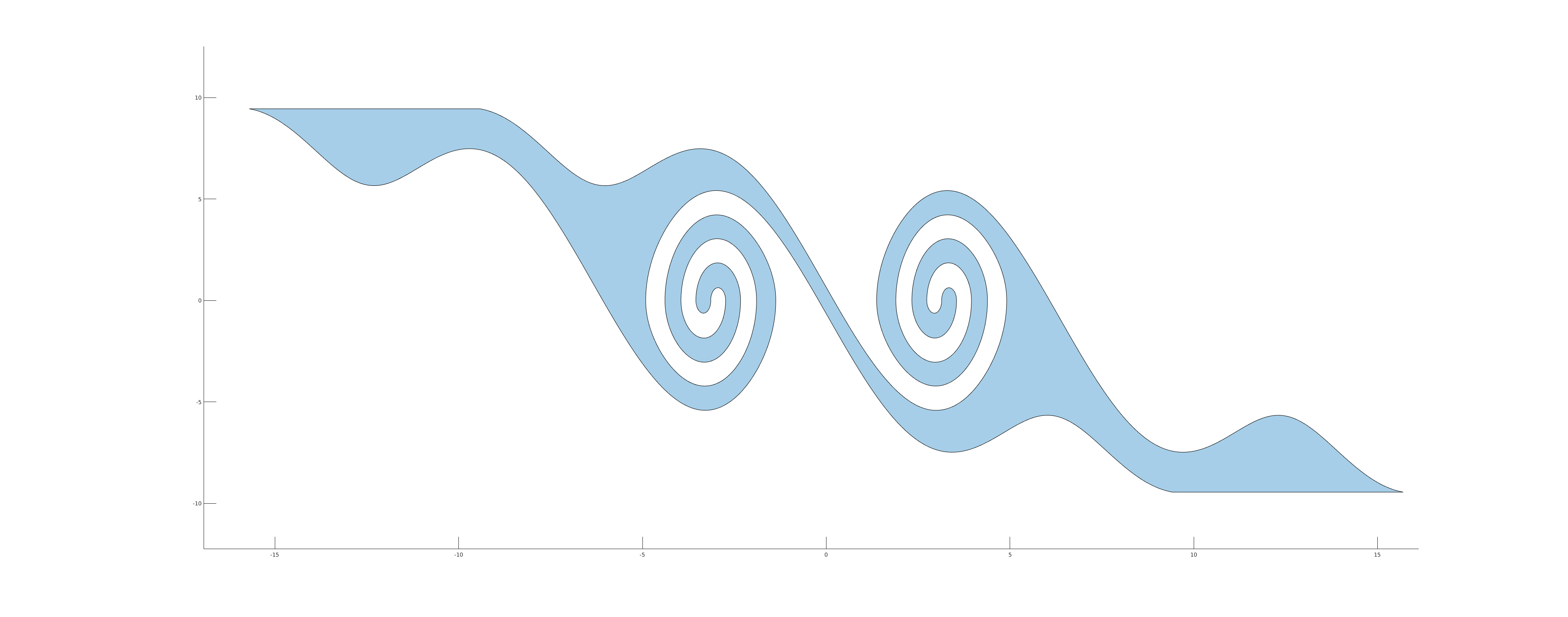
The finally intersection line looks like this: and it also the non-smooth line.

We developed a proof for the non-smooth line and provided it with a physical interpretation. Then we turned to the control-constrained case, which is much more complicated. The non-smooth line appears as follows:

Finally the HJB loss is really small. The value in the plot is Log(loss), we can see it is under 1e-5.

And we proof that under a low HJB loss we can guarantee a error bound on the true value function.

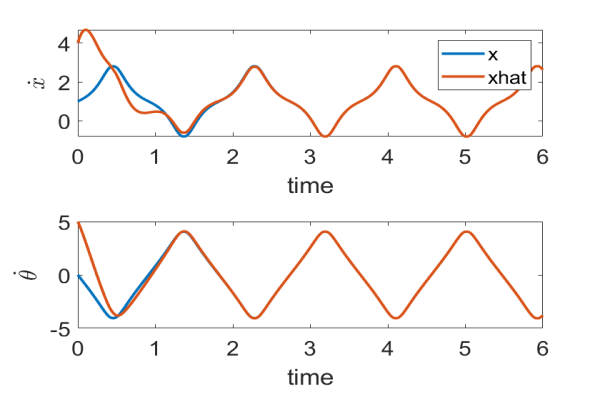
High-gain Observer Design

Transformed the dynamics of systems like cartpole, arcbot, and 3D rigid-body into high-gain standard forms and implemented the high-gain observer. Established a tighter bound for high-gain observer, showcasing its enhanced performance. Proved an error bound for residual dynamics using neural network approximation and validated the observer error on real robots, confirming it stayed within the set bound.

Observer notes(Download)

Cloth Shadow Art

The research focused on using differential simulation to design a square fabric with an arbitrary hole. When control inputs were applied, the dynamic shape of the hole matches a cartoon. The Finite Element Method (FEM) was implemented for cloth simulation, using StVK, ARAP, and bending energy models, with a comprehensive analysis of the Hessian, including 3D-2D projection differentiation. Various simulation methods like Implicit Euler, Explicit Euler, Projective Dynamics (PD), and Position Based Dynamics (PBD) were explored. A comparative study identified FEM as the most accurate method. Additionally, the study successfully optimized a waving wing example.

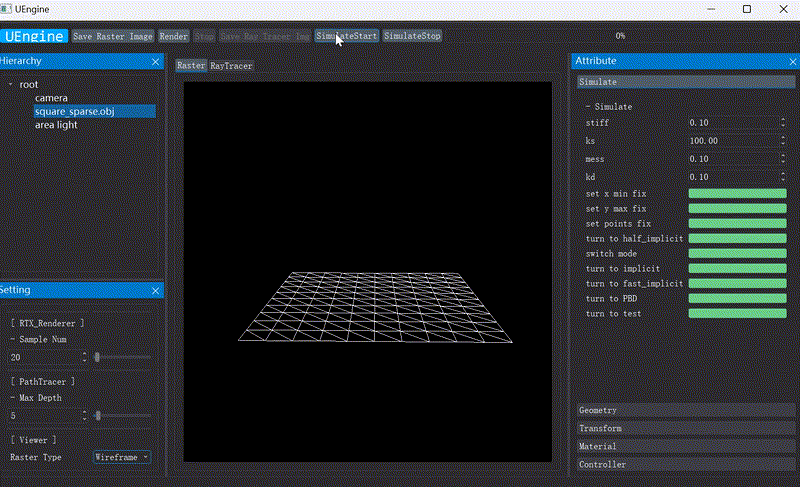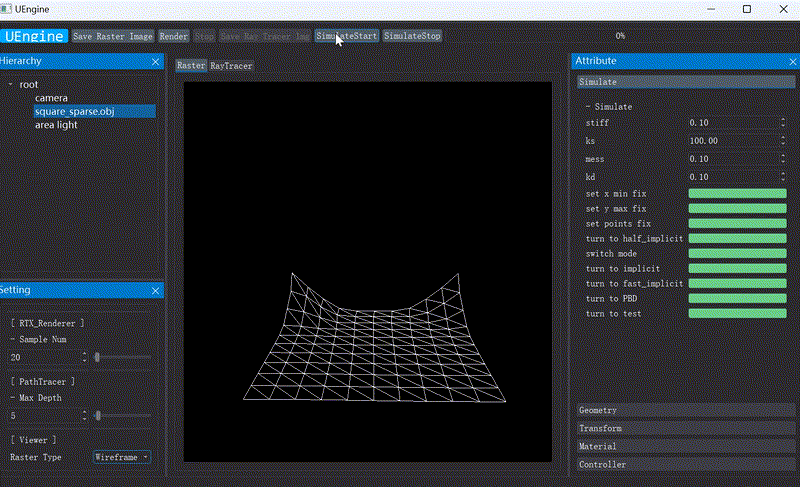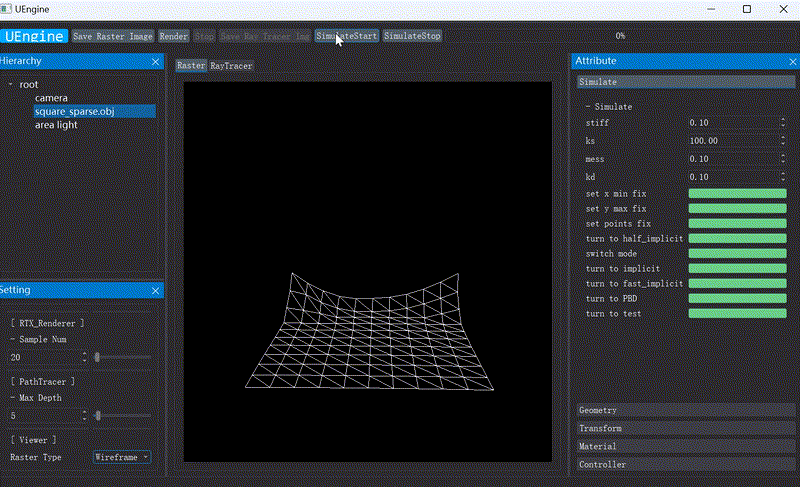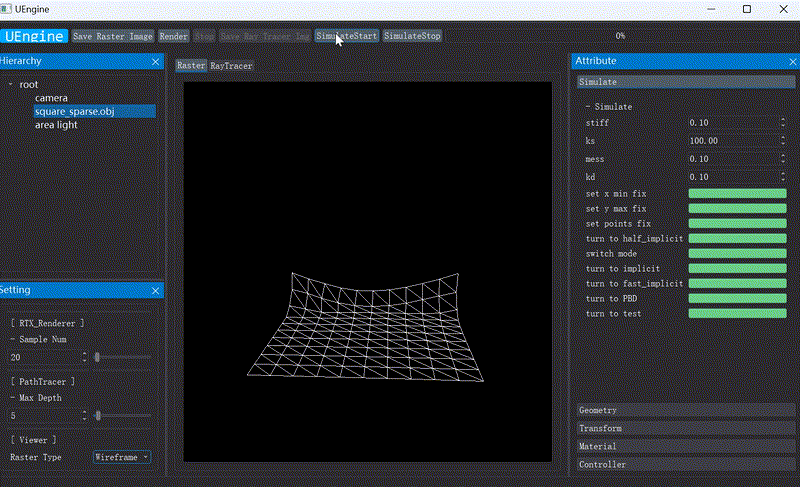
First I implement Implicit,Explicit euler method、PD(Projective Dynamics)、PBD(Position Based Dynamics) and FEM method. For differential simulation I first tried PD method with friction and contact, and analysed its property.

And then we turn to FEM, I derivate the FEM hessian matrix including a projection from 3D to 2D(while many previous work did not consider this)

I tried it on a simple example:

And finally tried it on a real example(see the top)

I am Haoyu Han, an incoming phd in Computational Robotics Lab at the School of Engineering and Applied Sciences (SEAS), Harvard University, advised by Professor Heng Yang. I am now interested in control and physical simulation. My previous experiences are about visualization and numerical computation, and I am eager to delve deeper into these topics. I have developed skills in ODE/PDE, Numerical Analysis, Control Theory, and Simulation.

See my github repository.

My research experience began in Computer Graphics (CG). I joined Graphics & Geometric Computing Laboratory (GCL) in USTC and first took online courses in CG. I honed my coding skills and became familiar with the classic topics in computer graphics. Subsequently, I conducted a survey on cloth simulation and implemented some classical methods. During this time I explored some ideas such as implementing unbalanced spring stiffness constants and applying wavelet analysis to cloth simulation. Following this, I delved into Differential Simulation and commenced a project on cloth shadow art.

When researching differential simulation, I gradually developed an interest in the topic of simulation in robotics and wanted to learn more about the field. This led me to start a summer internship at Harvard University, advised by Professor Heng Yang. During the internship, I first worked on observer to become familiar with some classical setting and techniques in robotics. I studied a book about observer and tried to apply it on various systems. This method is successful when applied to pendulum, cart-pole and arcbot, but not directly on quadrator. To deal with it, I introduced a new variable to transform it into high-gain form. Additionally I proofed a tighter bound of it.

Then I delved into optimal control problems with a continuous-time, infinite-horizon setting, starting from a pendulum example. It seems quite simple, right? But even for the pendulum, we found that it has some interesting properties. The value function at the lowest point must be non-smooth, because if the gradient exists, there would be a unique optimal control policy; however, in reality, the pendulum can swing either left or right. Furthermore, we drew and proved that there is a non-smooth spiral line in the value function. We then applied this to the control-constrained case and it proved to be much more interesting; some parts of the line appeared to be discontinuous! I conducted some analysis and provided a physical interpretation. Ultimately, we compared our methods with others and used the insights to guide neural network training. This experience gave me profound insights into how to explore a difficult problem, from reviewing related work to implementing and analyzing the topic, and finally finding a direction for further investigation.

My future plan is to develop theories that will guide computers and robotics in understanding and interacting with the real world through computational methods.